もう一つの歴史教科書問題おもしろ授業

多元史観による真実の日本古代史を求めてーー現在進行形の謎解き歴史ノンフィクション！地方史が変わる。日本史がくつがえる。

　授業前に生徒たちが夏休みの課題「読書感想文」の話題で盛り上がっていた。そこでつい「良い読書感想文を書くには」講座が始まった。

　「まず、良い読書感想文は本選びで８割が決まります……」

　これは読書感想文に限ったことではなく、「ボーリングは自分に合ったボール選びが８割」とか、「良い授業は教材選びと段取りで８割決まる」など。８割決定論はいろいろな分野で応用がきく。

　さて、物語文は主人公「誰々が何をする物語」というように要約することができる。例えば『ハリー・ポッター』であれば、主人公ハリーがヴォルデモートと戦う物語とでもまとめることができる。しかしそれはあくまでも外面的なストーリーである。物語にはこの外面的なストーリーと並行して内面的なストーリーが展開する。『ハリー・ポッター』の本質は、主人公ハリーが周囲の人々との関係性を通して内面的に成長していく物語なのである。著者は外面的なストーリーを描くのが目的ではなく、内面のストーリー展開を通じて自身の主張したいテーマを表現していくものなのだ。当然ながら良い読書感想文はその内面のストーリーに言及しているものである。

　そして、良い本選びとはその物語の内面のストーリーが読者自身の通過してきた心情の世界とオーバーラップする本を選ぶということである。そのようなベストマッチな本と出逢えれば８割方良い感想文が書けるものなのだ。もちろん残り２割は書き手の資質にもよる。

　実は『ハリー・ポッター』で読書感想文を書くのは、ちょっと難しさもある。それは『ハリー・ポッター』シリーズの中心テーマが聖書と関連しているからである。キリスト教のバックグラウンドがほとんどない日本人にとっては、理解しがたいかもしれなが、作者Ｊ・Ｋ・ローリングの作意をくみ取ると、そう思えて仕方がない。

　著者は喫茶店にコーヒー１杯でこもりながら、まず最終章第７巻のエンディングをイメージして執筆を始めたという。推察するに「死なんとする者は生きる」（マルコによる福音書8章35節）というイエスが語った聖書の中心的なメッセージが第７巻『ハリー・ポッターと死の秘宝』という作品に描かれていることから、そこに著者の主題が込められていると考えていいだろう。

　そして、第１～３巻に込められた「愛・信仰・希望」というテーマ。間違いなく彼女は１巻ごとに聖書的なメッセージを盛り込んでいる。「このように、いつまでも存続するものは、信仰と希望と愛と、この三つである。このうちで最も大いなるものは、愛である。」（コリント第一の手紙第１３章１３節）

　第１巻『ハリー・ポッターと賢者の石』では両親がいないことに寂しさを感じるハリーであったが、最終的に親から愛されていたということに気づき、試練を乗り越えていく。
　第２巻『ハリー・ポッターと秘密の部屋』ではピンチに陥った時にダンブルドア校長を信じることで強力な武器を取りだすことに成功し、危機を切り抜ける。
　第３巻『ハリー・ポッターとアズカバンの囚人』では、活力を吸い取ってしまう吸魂鬼(ディメンター) に取り囲まれ、希望を見出すことができないような絶望的な状況下で希望を持ち続け、守護霊の呪文を成功させて未来を切り開く。
　これまでに果たして『ハリー・ポッター』シリーズがキリスト教文学だと評論する人がいたであろうか？　私が書評を書くとしたら、声を大にして言いたい。『ハリー・ポッター』は最高のキリスト教文学であると。そして著者Ｊ・Ｋ・ローリングの純粋な動機を神様が良しとしたからこそ、これほどまでに全世界的にヒットしたのではないかという気がしてならない。

[5回]

2019/08/25 おもしろ授業 Comment(0)

ストーリー記憶術②「マーガリンを二重に乗っけると…」編

　"ストーリー記憶術①「豪華客船で仮面舞踏会」編"に続く第二弾。お待ちかね「マーガリンを二重に乗っけると…」編です。
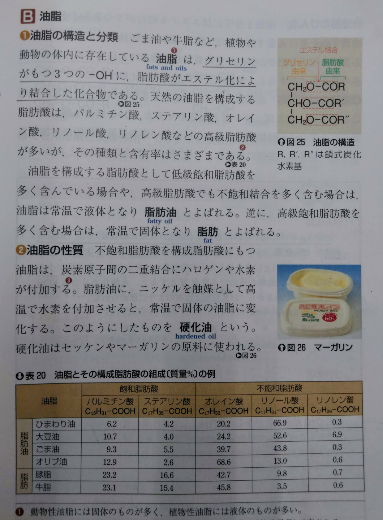
　皆さん、朝食はご飯派ですか、食パン派ですか？　食パンにはマーガリンを塗りますよね。「いや、ジャムを塗ります」なんて言わんといて下さい。ところで、食パンにマーガリンを二重に乗っけると付加価値が付いて高価になるという話を聞いたことがありますか?

マーガリンを二重に乗っけると
　　　　二重結合　ニッケル触媒
付加価値が付いて高価になる。
水素付加　　　硬化油

　二重結合を持つ脂肪油に、ニッケルを触媒として高温で水素を付加させると、常温で固体の油脂に変化します。このようにしたものを硬化油といいます。硬化油はせっけんやマーガリンの原料に使われます。

[1回]

2019/08/01 おもしろ授業 Comment(0)

ストーリー記憶術①「豪華客船で仮面舞踏会」編

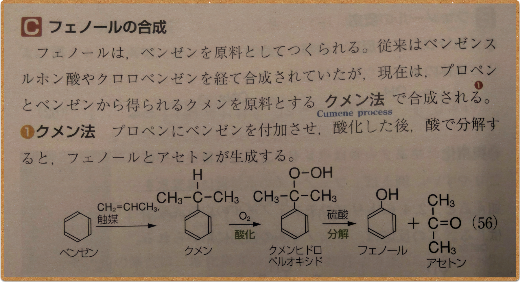
　高校３年生の皆さん、化学の授業も大詰めとなってきました。もう有機化学で芳香族化合物について勉強しましたか。今回はフェノールの製法について、ストーリー記憶術にチャレンジしてみましょう。物語の流れに沿って記憶する方法です。
　ロペルさんが豪華客船で開かれる仮面舞踏会に参加して、友達の龍さんに会いました。そんな情景を思い浮かべて下さい。

＜フェノールの製法＞
便座にプロペラ付けて仮面を作り、
ベンゼン＋プロペン　→　クメン
仮面舞踏会に参加したら、「仮面ひどっ、ロペルおかしいど」
クメンを酸化　→　クメンヒドロペルオキシド
と龍さんに一刀両断。「船乗るのにあせっとん？」
硫酸で分解　→　フェノール＋アセトン

[1回]

2019/06/28 おもしろ授業 Comment(0)

化学基礎ーー混合物の６つの分離法

　自然界に存在するものは大半が２種類以上の物質が混じり合った混合物の状態で存在しています。そのような混合物から純物質を分離するには大きく６種類の方法があります。「ろくろ再上昇中」と覚えてください。

ろ……ろ過
くろ…クロマトグラフィー
再……再結晶
上……蒸留（分留）
昇……昇華
中……抽出

　ところで、「ろくろ」って知っていますか？　砥部焼で有名な愛媛県伊予郡の砥部町に行くと陶器作り体験をさせてくれますよね。粘土をこねて、ろくろを回しながら陶器の形を造っていきますが、そのろくろが再上昇しているところをイメージしてみたら覚えやすいでしょう。

　「陶器を造る者は、同じ土くれから、一つを尊い器に、他を卑しい器に造りあげる権能がないのであろうか」（ローマ人への手紙第９章21節）

　喩えるなら、陶器を造る人が同じ土くれから尊い器と卑しい器を造り分けるように、混合物から純物質を分ける操作が分離なのです。

　また、どのような金属イオンが含まれているかを調べるには炎色反応を利用します。覚え方は有名で、色々とありますが、昔ながらの簡単かつ田舎っぽいバージョンを教えましょう。“Simple is the best.”です。

リアカー　無き　K村の　加藤は　馬力で　努力　するべー

Li (赤)　Na (黄)　K (紫)　Ca (橙)　Ba (黄緑)　Cu (青緑)　Sr (紅)

[2回]

2019/06/13 おもしろ授業 Comment(0)

ほっそん先生のクジラの話

　ホームページ『新古代学の扉』を見ていたら、懐かしい名前が飛び込んできた。いつの間に掲載されていたのか、もう明日の事である。

（関西）古田史学講演会　案内・報告を仮設置

４月２６日（金）18時45分～20時15分、誰も知らなかった古代史での細川隆雄氏講演案内

誰も知らなかった古代史の会

　第３７回講演

鯨から日本の古代を探る

-- 神武歌謡『くぢら障る』歌と万葉集『調使首のイサナトリ』歌を中心に

講師　細川隆雄（愛媛大学名誉教授）

２０１９年　４月２６日　18時45分～20時15分

参加費は500円

会場はアネックスパル法円坂（大阪市教育会館）3階第3会議室

交通はＪＲ大阪環状線及び大阪メトロ森ノ宮駅、西に徒歩10分（中央線谷町4丁目から東に10分）難波宮跡の東隣り

　「ほっそん先生」こと細川隆雄氏にお会いしたのは昨年のことだったろうか。愛媛大学農学部名誉教授で専門はソ連の農林水産業であるが、いつしかクジラ博士と呼ばれるようになつた。『鯨塚からみえてくる日本人の心』シリーズや『ほっそん先生鯨に恋をする』など、鯨に関する著作も多い。
　私自身も高岡郡佐川町の鯨坂八幡宮のルーツ(鯨坂八幡宮との関係ーー安芸郡の田野八幡宮)を追いかけて、古くから鯨漁が盛んであった安芸郡調査に乗り出し、鯨塚の存在も知るようになった。細川先生からは色々と教えを請いたいところである。
　勝手ながら講演会のＰＲを兼ねて紹介させていただいた。神武歌謡と万葉集を中心材料として、日本の古代の謎にアプローチする、めったに聞けない鯨と古代日本人の密接な関係を知る内容となりそうだ。

[1回]

2019/04/25 おもしろ授業 Comment(0)

今こそチコちゃんに問いたい――なんで師管は「師」管と書くの？

　中１の理科２分野「植物のからだのつくり」で茎の断面図が出てくる。ホウセンカなどの双子葉類の場合、根から赤色の水を吸収させると形成層より内側の管が赤く染まることから、水や肥料分の通る道管が内側にあることが分かる。水が通る管であるから「水―道管」と覚える。

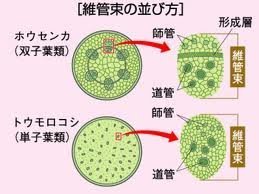
　一方、光合成により葉で作られた養分が運ばれる管は形成層の外側にあり、師管と呼ばれる。ところで師管の「師」って、どうして教師や師匠の「師」なの？　ちょっと「イミフ（意味不明）」ではないですか。話はそれますが、東北地方の県名は「ああイミフや」と覚えます。青森県・秋田県・岩手県・宮城県・福島県・山形県の６県です。頭文字をつなげてみて下さい。覚え方なので深い意味はありません。

　本題に戻ろう。なんで師管は「師」管と書くのか？　ＮＨＫ総合テレビ『チコちゃんに叱られる』（毎週金曜午後7時57分 | 再放送毎週土曜午前8時15分）に投稿してみたい内容である。

　「ねー岡村、この中で知ったかぶりの教師面している大人って誰？」

　5才のチコちゃんが上記の問いをゲストに投げかける。知らないでいると、チコちゃんに「ボーっと生きてんじゃねーよ！」と叱られることになる。

　このクイズ、もう１０年ほど前から理科の授業で使っているネタの一つで、正しいかどうか、はっきりとは分からないが、たぶんこうだろうという結論を得ている。当然ながら、生徒に質問してもまともな答えは返ってこない。テストでは「師管」と書けば○がもらえるからと丸暗記して、その意味まで深く考えていない学生がいかに多いことか。

　でも、チコちゃんは知っています。なんで師管は「師」管と書くのか。――師管はもともと「篩（ふるい）管」と書いていたから。

　師管の構造を詳しく見てみると、管の途中に穴のあいたしきり板のようなものがある。まるで篩のようである。ケーキを作る時に小麦粉にだまができないようにふるいにかけるあの篩である。その構造をよく表した表記として師管のことを昔は「篩管」と言っていたが、「篩」は当用漢字にないため、竹冠を除いた「師」の字を当てて「師管」と書き表すようになった。すなわち、篩は古い漢字だから「師管」と表記されるようになって、その意味がわからなくなったのではないだろうか。

[13回]

2019/04/18 おもしろ授業 Comment(0)

安田亨のリスペクトする池見酉次郎先生

　東大受験では定番となっている『東大数学で1点でも多く取る方法理系編』シリーズ。著者の安田亨氏がリスペクト（尊敬）する人物が本の裏表紙に紹介されている。

　座右の銘は「汝まず世界の必要とするものとなれ。さすれば、たとえ森の中に住むといえども汝の戸口に人々が集まるであろう（元は思想家Ralph Waldo Emersonの言葉。九州大学名誉教授・池見酉次郎先生が座右の銘としておられるのを本で見て）」

　おそらく『セルフコントロールの医学』(池見酉次郎著、1978年) 辺りの本を読んでのことではないかと推察する。私自身も池見酉次郎(いけみゆうじろう、1915ー1999年) 先生とは縁があって、特に医学部を目指す生徒には紹介することもある。

　池見先生は日本の心身医学、心療内科の基礎を築いた草分け的な日本の医学者であった。医学部を志したきっかけは、自らの吃音の悩みがあったからとも聞く。そしてアメリカにも渡り、エマーソンの言葉の真意を直接質問したという。その答えは意外にも「良いネズミ捕りがあれば森の中でも買いに来る」といったニュアンスだったらしい。
　20年ほど前に、池見酉次郎先生の訃報を知り、先生とお話した内容が思い返された。1991年頃だったろうか。当時、池見先生から実存的転換について伺った。ドクターからなぜ哲学？　と思われるかもしれないが、そこに心療内科（ホーリスティック医学）の真髄があると感じさせられた。
　末期ガンの患者で、まれにガンの退縮が起きることがあるという。そのような患者さんに話を聞くと、共通する体験があった。それまでは自分の力で生きてきたと思っていたが、死に直面した時に「大自然の中で、生かされて生きている自分であった」ことに気付かされたというのだ。ーーこれこそまさに実存的転換である。
　恥ずかしながら、当時は実存的転換の意味すらよく知らなかった。その後、ショーペンハウアーやキルケゴールなどの実存主義哲学へと目を開かされる契機にもなった。
　医学部志望の生徒が増える昨今。単なる合格請負人にはなりたくない。世の中から必要とされる人物を送り出していきたいものだ。さすれば地方大学といえども、汝の戸口に人々が集まるであろう。

[3回]

2019/02/06 おもしろ授業 Comment(0)

忘れた時にはギャル曽根の本名を

　中学２年生の理科で、化学変化について勉強する。まず最初に「なぜカルメ焼きは膨らむか？」といったテーマで、炭酸水素ナトリウムの熱分解（加熱による分解）などを学んだりする。

Ｑ.　次の（　）に入る化学式を答えよ。
炭酸水素ナトリウム→炭酸ナトリウム＋水＋二酸化炭素
2NaHCO3→（　　）+　H2O　+　CO2

　上記の化学反応式は高校化学でもよく出てくるので、覚えていたら役立つ場面が多い。しかし、忘れている人も多いのが現実だ。そこで「炭酸ナトリウムの化学式、忘れたときにはギャル曽根の本名を思い出したらいい」と切り札を出す。

　「そう、曽根菜津子さん（Na2CO3
）」
　さすがに本名（曽根は旧姓、結婚して名城）までは知らない生徒が多いが、ギャル曽根が今でもテレビで活躍中なので、まだまだ使えるネタである。結婚する前のギャル曽根時代から、かれこれ10年ほど授業で使わせていただいている。

　ちなみに「なぜカルメ焼きは膨らむか？」のほうは、ふくらし粉の主成分が炭酸水素ナトリウムであり、熱分解によって二酸化炭素が発生するためである。よく言うじゃないですか。気体(期待)に胸膨らませるって……。
　また、大河ドラマ『いだてん』では、主人公・金栗四三(しそう)の父親が病弱で、いつも重曹(じゅうそう)水を飲んでいた。この重曹も炭酸水素ナトリウムのことで、胃酸過多など対して弱アルカリ性の炭酸水素ナトリウムで胃酸を中和する効果がある。
　重曹(炭酸水素ナトリウム)１つとっても、まさに重層構造の知識を教える教材となるのだ。

[1回]

2019/01/20 おもしろ授業 Comment(0)

2018年最後のメッセージ

　今年の年頭に次のような話をした。「2018年は喜びも悲しみも二人で分かち合えば感謝の思いがあふれてきます。2018÷2=1009(Thank you!)」。年末最後の授業でも、数名の生徒に同じメッセージを伝えた。反応はまずまずであった。

　私個人としても、今年一年間は良き理解者に巡り合わせていただき、不思議な縁も感じることが多かった。お世話になった方々に感謝の思いを伝えたい。
　ほとんどの日本人は人に対して感謝するが、敬天思想を持つ韓国人は誰に対して「ありがとう」と言うか？　神様にだ(カムサムニダ)！

[1回]

2018/12/31 おもしろ授業 Comment(0)

勝海舟は2次方程式を勉強した

「方程式の中で“７色の方程式”と言われるものは何でしょうか？」
　「2次（虹）方程式」
　朝、ラジオから「勝海舟は2次方程式を学んだ」という話が聞こえてきた。勝海舟と言えば大河ドラマ『西郷どん』でもキーマンになっていたが、江戸城無血開城に一役買った幕府の重鎮である。何の話かというと、ゆとり教育に対する反論のようであった。
　「数学で2次方程式を勉強しても、大人になって実際に使う場面はない。そんなものを学ぶ必要があるのか？」というゆとり教育推進派の主張があった。現役の生徒たちも時々、声高々に訴えることがある。

　勝海舟にとっても、2次方程式が実際に役立つ場面はなかったかもしれない。しかし思考力を鍛えることに意味があるという。2次方程式の解法には、①平方根の利用　②因数分解　③解の公式ーー大きくはこの３つがある。それらをケースバイケースで使い分けなければならない。江戸城無血開城というイギリスの名誉革命にも並び評価される決断は、賢明な判断力あったればこそであろう。
　考えることはエリートに任せて、一般人は結論を受け入れさえすれば良い……。世の中がそんな風潮にならないためにもしっかりと学ぶ必要あり、といったコメンテーターの主張であったように思う。

[0回]

2018/10/23 おもしろ授業 Comment(0)

≪ Before ｜HOME｜ Next ≫

カレンダー

2025/04